UVa Online Judge Challenge "11045"
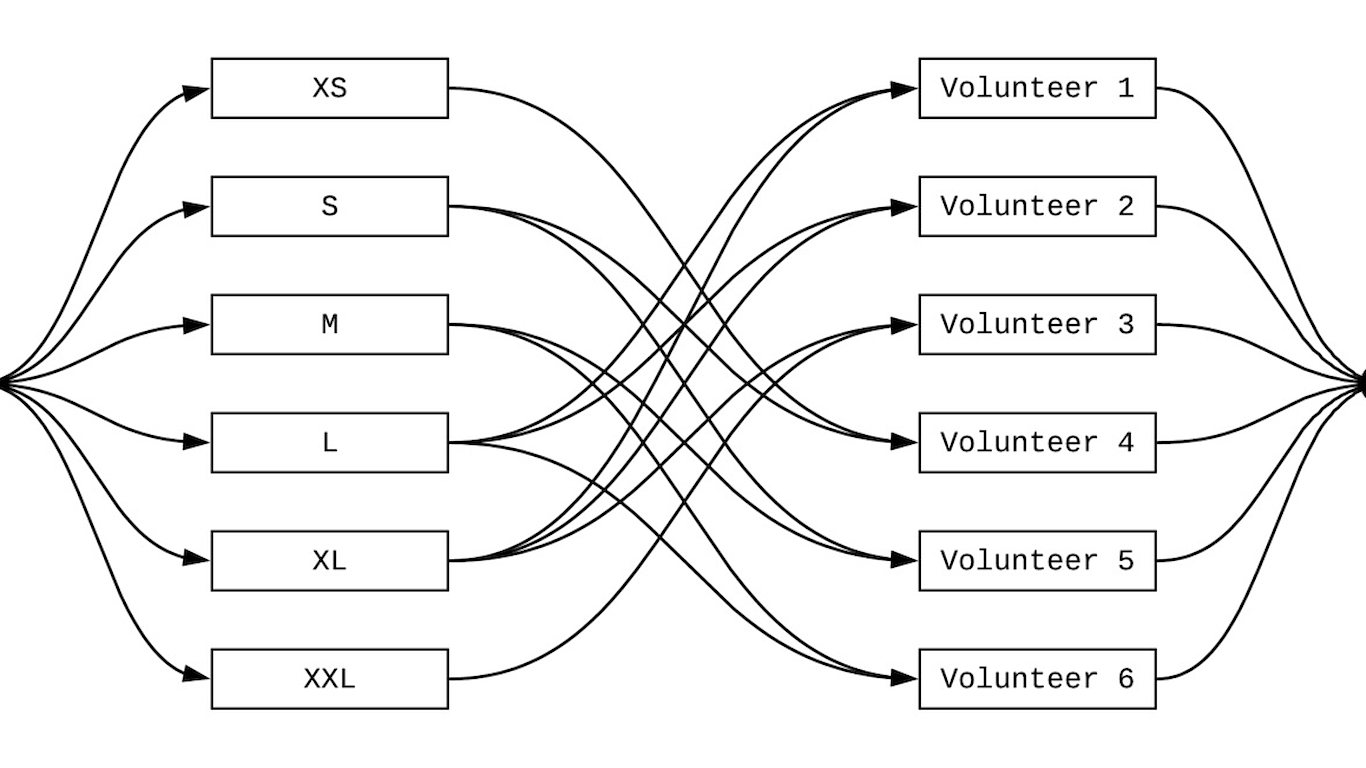
This is a maximum flow problem on a bipartite graph. I created the flow chart above to visualize the 3 test cases. The virtual judge run time was 0.18s.
Problem
Solution
1/* * * * * * * *
2Tristan Madden
32018-05-01
4https://onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1986
5* * * * * * * * */
6
7import java.io.BufferedReader;
8import java.io.IOException;
9import java.io.InputStreamReader;
10import java.util.Arrays;
11import java.util.HashMap;
12import java.util.LinkedList;
13import java.util.Queue;
14public class Main {
15 static int source = 0;
16 static int sink = 1;
17 static HashMap<String, Integer> map = new HashMap<>(6);
18 public static void main(String[] args) throws IOException {
19 map.put("XS", 2);
20 map.put("S", 3);
21 map.put("M", 4);
22 map.put("L", 5);
23 map.put("XL", 6);
24 map.put("XXL", 7);
25 BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
26 int testCases = Integer.parseInt(br.readLine());
27 while (testCases-- > 0) {
28 String[] nm = br.readLine().split(" ");
29 //N is multiple of 6, 1 ≤ N ≤ 36
30 int N = Integer.parseInt(nm[0]);
31 //M, 1 ≤ M ≤ 30, indicates the number of volunteers, with N ≥ M
32 int M = Integer.parseInt(nm[1]);
33 /* * * * * * * * * * * * * * * * * * * * *
34 |* The size of the graph will be the sum of:
35 |* -the number of shirt sizes available (6)
36 |* -the number of volunteers (M)
37 |* -the sink and source (2)
38 |* * * * * * * * * * * * * * * * * * * * */
39 MyGraph graph = new MyGraph(M + 8);
40 /* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
41 |* S T E P O N E
42 |* Construct the edges from the source node to the t-shirt nodes.
43 |* The capacity of these edges will be N/6, or the number of t-shirts
44 |* in stock of this size.
45 |* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * */
46 int t;
47 for (t = 0; t < 6; t++) {
48 graph.addEdge(source, t + 2, N / 6);
49 }
50 /* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
51 |* S T E P T W O
52 |* Construct the edges from the t-shirt nodes to the volunteer nodes.
53 |* This is the bipartite graph.
54 |* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * */
55 int i, a, b;
56 for (i = 0; i < M; i++) {
57 String[] sizes = br.readLine().split(" ");
58 a = map.get(sizes[0]);
59 b = map.get(sizes[1]);
60 graph.addEdge(a, i + 8, 1);
61 graph.addEdge(b, i + 8, 1);
62 }
63 /* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
64 |* S T E P T H R E E
65 |* Construct the edges from the volunteer nodes to the sink node.
66 |* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * */
67 int v;
68 for (v = 0; v < M; v++) {
69 graph.addEdge(v + 8, sink, 1);
70 }
71 /* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
72 |* S T E P F O U R
73 |* Run Max Flow on the bipartite graph.
74 |* If the maximum flow is equal to the number of volunteers, print
75 |* "YES". Otherwise, print "NO".
76 |* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * */
77 if (graph.maxFlow(source, sink) == M) {
78 System.out.println("YES");
79 } else {
80 System.out.println("NO");
81 }
82 }
83 }
84}
85class MyGraph {
86 int size;
87 int[][] edges;
88 MyGraph(int _size) {
89 this.size = _size;
90 this.edges = new int[size][size];
91 }
92 void addEdge(int x, int y, int weight) {
93 edges[x][y] += weight;
94 }
95 /* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
96 |* M A X F L O W
97 |* This is a franken-method pieced together from other solution I found
98 |* online. Pretty much treating it as a black box.
99 |* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * */
100 int maxFlow(int source, int sink) {
101 int[] prev = new int[size];
102 int answer = 0;
103 int mincut = Integer.MAX_VALUE; //infinity
104 while (true) {
105 Queue<Integer> q = new LinkedList<>();
106 q.add(source);
107 Arrays.fill(prev, -1);
108 while (!q.isEmpty() && prev[sink] == -1) {
109 int u = q.remove();
110 for (int v = 0; v < size; v++) {
111 if (v != source && prev[v] == -1 && edges[u][v] > 0) {
112 q.add(v);
113 prev[v] = u;
114 }
115 }
116 }
117 if (prev[sink] == -1) {
118 break;
119 }
120 int y = sink;
121 int x = prev[y];
122 while (x != -1) {
123 mincut = Math.min(mincut, edges[x][y]);
124 y = x;
125 x = prev[y];
126 }
127 int v = sink;
128 int u = prev[v];
129 while (u != -1) {
130 edges[u][v] -= mincut;
131 edges[v][u] += mincut;
132 v = u;
133 u = prev[v];
134 }
135 answer += mincut;
136 }
137 return answer;
138 }
139}