UVa Online Judge Challenge "11045"
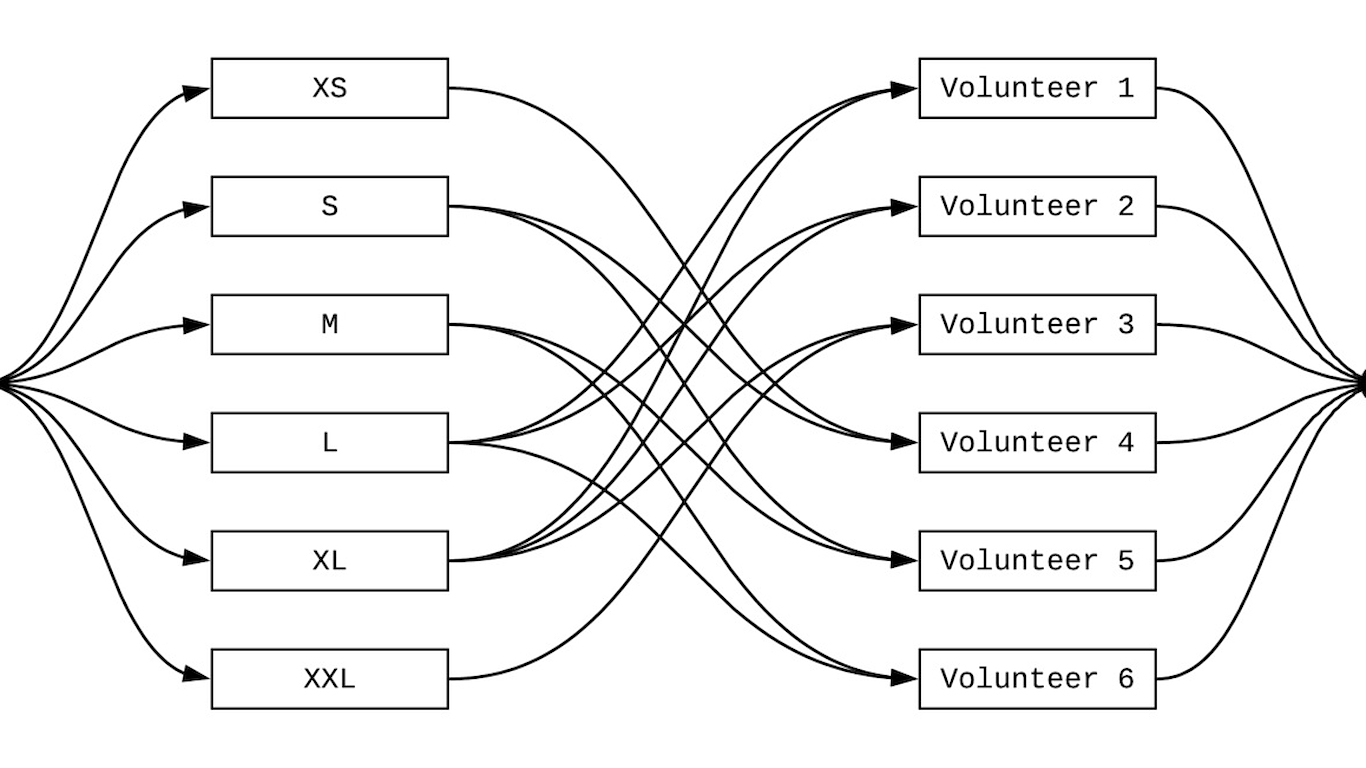
This is a maximum flow problem on a bipartite graph. I created the flow chart above to visualize the 3 test cases. The virtual judge run time was 0.18s.
Term View
Uva
Entries linked to "Uva" across the quiet archive.
Entries
9
Categories
23
Tags
187
UVa Online Judge Challenge "10305"
This problem presents a DAG and the solution requires implementing a topological sort. I noticed that a topological sort can be implemented using only boolean arrays so I used this as an opportunity to finally get around to using Java’s BitSet class. The virtual judge run time was 0.050s.
UVa Online Judge Challenge "572"
Although BFS and DFS were recommended solutions to the problem, I saw an opportunity to solve this problem using Disjoint Sets. The virtual judge run time was 0.050s.
UVa Online Judge Challenge "1112"
This problem involves a relatively small graph, so I opted to implement the Floyd-Warshall Algorithm instead of Dijkstra’s Algorithm for the sake of simplicity. This algorithm finds the shortest path between every pair of vertices in a graph, running in O(n^3) time. Although this might sound inefficient, the UVA judge accepted this program with a runtime of 0.12 seconds, which is well within the 3-second threshold. I designed this algorithm using an object-oriented approach and avoided arrays, so that if I ever have enough free time, I can easily integrate it into Processing and visualize it in 3D.
UVa Online Judge Challenge "10550"
“Now that you’re back to school for another term, you need to remember how to work the combination lock on your locker. A common design is that of the Master Brand, shown at right. The lock has a dial with 40 calibration marks numbered 0 to 39. A combination consists of 3 of these numbers; for example: 15-25-8. To open the lock, the following steps are taken…”
UVa Online Judge Challenge "272"
“TEX is a typesetting language developed by Donald Knuth. It takes source text together with a few typesetting instructions and produces, one hopes, a beautiful document. Beautiful documents use…”
UVa Online Judge Challenge "10110"
“There is man named ”mabu” for switching on-off light in our University. He switches on-off the lights in a corridor. Every bulb has its own toggle switch. That is, if it is pressed then the bulb turns on. Another press will turn it off. To save power consumption (or may be he is mad or something else) he does a peculiar thing. If in a corridor there is n bulbs, he walks along the corridor back and forth n times and in i-th walk he toggles only the switches whose serial is divisable by i. He does not press any switch when coming back to his initial position. A i-th walk is defined as going down the corridor (while doing the peculiar thing) and coming back again. Now you have to determine what is the final condition of the last bulb. Is it on or off?”
UVa Online Judge Challenge "100"
“Problems in Computer Science are often classified as belonging to a certain class of problems (e.g., NP, Unsolvable, Recursive). In this problem you will be analyzing a property of an algorithm whose classification is not known for all possible inputs. Consider the following algorithm…”
UVa Online Judge Challenge "11172"
“Some operators checks about the relationship between two values and these operators are called relational operators. Given two numerical values your job is just to find out the relationship between them that is (i) First one is greater than the second (ii) First one is less than the second or (iii) First and second one is equal.”
Browse Routes
Adjacent collections
- Posts108
- Prompts2
- Archive16
- Categories23
- Tags187
Discovery Layer
Memory Field
A secondary exploration surface for following relationships beyond the visible ledger.
Matching entries